Дискретизация конструкции

Каждый I – й элемент в составе тела или конструкции может испытывать в дополнение к усилиям взаимодействия со смежными конечными элементами действие поверхностных (по граням элемента) и объёмных внешних нагрузок.

Тогда уравнение движения можно записать в форме уравнений статического равновесия, если внешние возмущающие силы, приложенные к рассматриваемому элементу, дополнить соответствующими данному элементу силами инерции и силами сопротивления

p*(x, y, z, t) = p(x, y, z, t) -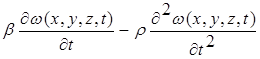 (2.3.5.1)

где р (х, у, z, t) — интенсивность внешних возмущающих сил; w (х, у, z, t) — компонент перемещения; р — плотность материала тела.

Распределенная нагрузка (2.3.5.1) в методе конечных элементов заменяется статически эквивалентными им сосредоточенными усилиями, приложенными в узловых точках. Совокупность этих узловых усилий образует вектор

P* = {P1*, P2*, …, Pr*}. (2.3.5.2)

Компоненты вектора Р* можно определить с помощью известного правила механики для вычисления обобщенных сил. Пусть поле перемещений для рассматриваемого конечного элемента приближенно аппроксимируется выражением

w(x, y,z,f) = Nk(x,y,z)qk(t), (2.3.5.3)

или в матричной форме

w(x, у, z, t) = Nq, (2.3.5.4)

где N = [Nlt N.г, ., Nr ] — матрица-строка, элементами которой являются известные для конечного элемента рассматриваемого типа функции.

Если теперь узловым перемещениям qk сообщить малые приращения δqk, то перемещения по объёму конечного элемента также

получат приращения

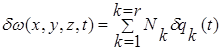. (2.3.5.5)

Работа нагрузки Р* (х, у, z, t) на приращениях перемещений 8w равна сумме работ узловых усилий Pk на соответствующих каждой из этих сил приращениях узловых перемещений:

. (2.3.5.6)

Откуда, если воспользоваться выражением (3.5.5),

k = 1, 2,…, r, (2.3.5.7)

Подставляя в правую часть выражение (3.5.2) для р* получаем

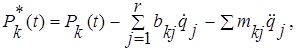k = 1, 2, …, r, (2.3.5.8)

где

(2.3.5.9)

Систему выражений (2.3.5.8) для i-го элемента можно представить в виде одной матричной зависимости

(2.3.5.10)

где— так называемые матрица сопротивления и матрица масс конечного i'-го элемента.

Прежде чем переходить к изложению следующего этапа МКЭ, поясним понятие местной и общей системы координат.

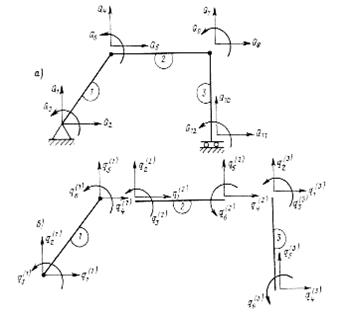
Рис.2.3.6.1. Плоская стержневая рама

До сих пор все используемые нами величины имели дополнительный индекс — номер конечного элемента. И, следовательно, для определения положения любого элемента, например матрицы q(l) = =,нужно указать порядковый номер элемента среди других элементов матрицы и номер конечного элемента (q(s'}). Аналогично поступаем и для прямоугольных матриц:— jk-й элемент матрицы B(i).

На рис.2.3.6.1, а показана плоская стержневая рама. Предположим, что при расчете такой рамы по МКЭ она была расчленена на три конечных элемента. На рис.2.3.6.1,б указаны обозначения отдельных элементов векторов узловых перемещений конечных элементов рамы q(1), q(2) и q(3). Видим, что использованная форма обозначения не включает наличия каких-либо взаимосвязей между смежными конечными элементами. Принято именовать такую систему обозначений системой обозначений в местной системе координат конкретного 1-го конечного элемента.

Вместе с тем, в силу непрерывности линейных перемещений и углов поворота сечений, значения этих величин в узловых точках; принимаемые нами в МКЭ за основные неизвестные, также непрерывны и, следовательно, не зависят от «принадлежности» узловой точки к тому или иному примыкающему к ней конечному элементу.

Введем вектор основных неизвестных (перемещения узловых точек) всей рамы (см. рис. 2.3.6.1, а)

Q={Q1, Q2, Q3, …,Q12} (2.3.6.1)

В отличие от векторов q(l\ i = 1, 2, 3 вектор Q принято называть вектором узловых перемещений в общей системе координат (для всей рассматриваемой конструкции).