Дискретизация конструкции
Между отдельными элементами вектора перемещений в местной
системе координат
q = {q(1) q(2) q(3)} (2.3.6.2)
и вектором Q существуют определенные связи, например:
и т. д. (2.3.6.3)
Эта связь
q = HQ (2.3.6.4)
т. е. значение матрицы H, устанавливается путем непосредственного рассмотрения векторов q и Q.
Для составления уравнений равновесия конструкции в целом воспользуемся принципом возможных перемещений, согласно которому сумма всех сил, (внешних и внутренних), действующих на конструкцию, на любом ее возможном перемещении равна нулю:
(2.3.7.1)
или, если учесть выражения (2.3.4.1) и (2.3.5.10),
= 0, (2.3.7.2)
где 
] - квазидиагональная матрица жесткости конструкции в местной системе координат; Ве=[В(])В(2)… В(ы)] — квазидиагональная матрица сопротивления в местной системе координат; Mg = [M(1) M(2)…M(M)] — квавазидиагональная матрица масс в местной системе координат q = {q(1) q(2)…q(M)} — вектор узловых перемещений конструкции в местной системе координат; Р= {P(1)P(2)…P(M)} — вектор внешних узловых перемещений в местной системе координат.
Элементами выписанных выше матриц служат соответствующие матрицы (векторы) конечных элементов конструкции.
Если теперь учесть зависимость (2.3.6.4) и принять во внимание произвольность элементов вариации δQT, то получим искомое матричное уравнение движения рассматриваемой конструкции
(2.3.7.3)
где
(2.3.7.4)
— матрицы масс, сопротивления и жесткости всей конструкции в общей системе координат. Размер этих матриц равен л х п, где п — число неизвестных в общей системе координат;
F = HTP. (2.3.7.5)
- вектор -столбец размером п х 1. Его элементы характеризуют внешнее воздействие на конструкцию.
Для нелинейных задач матрицы М*, В*, К* в уравнении (2.3.7.3) зависят от искомых узловых неизвестных.
Полученное уравнение (2.3.7.3) эквивалентно системе п дифференциальных уравнений второго порядка, описывающих движение упругой системы с п степенями свободы.
Уравнение (2.3.7.3) полностью идентично уравнению
где A – матрица масс; B – матрица сопротивления; C – матрица жёсткостей.
Если воспользоваться гипотезой Сорокина
(2.3.7.6)
где 
коэффициент неупругого сопротивления материала; 
коэффициент поглощения. достаточно матрицу внешнего сопротивления B(i) для i – го конечного элемента заменить матрицей B*(i) элементы которой определяются из зависимости
Решение задач по снижению виброакустической активности пилона следует начинать на этапе проектирования по нескольким причинам. Во-первых, на готовой продукции, устранение или снижение вибраций возможно лишь ограниченными средствами, а во-вторых, на этапе проектирования возможно воздействие на ожидаемые динамические характеристики путем изменения инерционных, жесткостных, геометрических и силовых параметров.
Конструкция пилона представляет собой трубу овального сечения с размерами полуосей а = 1200 мм, в = 430 мм, толщиной стенки 20 мм, и обтекатель, собранный из пластин толщиной 20 мм.
Целью данного проекта является проверка данных полученных при эксперименте реального водозаборника с помощью пакета для твердотельного моделирования SolidWorks. Собственные частоты полученные для пилона в эксперименте являются следующими: первая низшая форма для водозаборника в воздухе равна f1=32,5 Гц, вторая форма f2=81,0 Гц, третья f3=86,5 Гц.
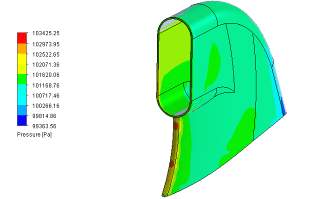
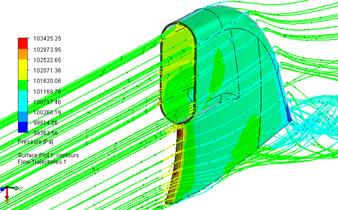
Продуем данный пилон изображенный на рис. воздухом со скоростью 30-50 м/с и внешним давлением окружающей среды равным одной атмосфере.
Полученные результаты по пилону представлены ниже на рис.2.4.1.1 и рис.2.4.1.2.
На рисунках наглядно видно как распределяется поток вдоль поверхности водозаборника. Можно проследить как поток воздуха воздейсвует на конструкцию и какие возникают при этом давления на поверхности пилона.
