Создание упрощенной математической модели движения судна, управляемого рулем и винтом

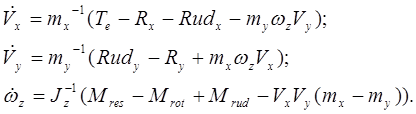
где

V x,y - проекции вектора линейной скорости судна на продольную и поперечную оси соответственно;

wz - проекция вектора скорости вращения на вертикальную ось, характеризующая рыскание судна;

x,y ,z - соответствующие ускорения;

mx,my - присоединенные массы относительно продольной и поперечной осей соответственно;

Jz - присоединенный момент инерции относительно вертикальной оси;

mx = (1+k11)D,

my = (1+k22)D,

Jz = (1+k66)Jzz;

kij - соответствующие коэффициенты присоединенных масс и моментов;

D - водоизмещение судна;

Jzz - момент инерции судна относительно вертикальной оси;

Входными величинами системы (1) являются число оборотов винта и угол перекладки руля.

Выходными величинами являются составляющие вектора скорости судна - Vx, Vy, скорость вращения судна вокруг вертикальной оси Z - wz, курс судна К, радиус кривизны поворота Rs, угол дрейфа судна b и координаты судна в прямоугольной, не связанной с центром тяжести, системе координат x1, y1.

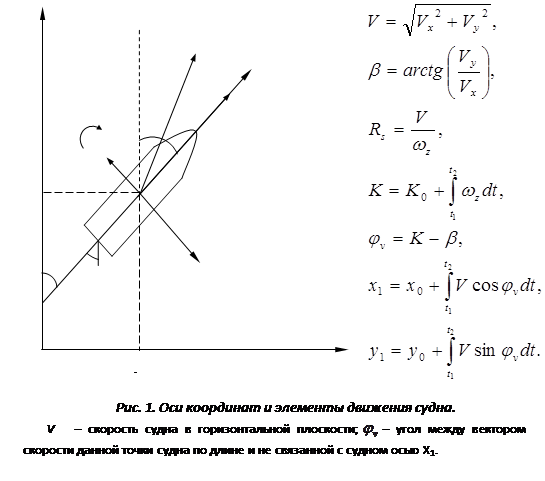
На рис. 1 приведены оси координат и элементы движения судна в горизонтальной плоскости, а также уравнения связи, используемые для получения некоторых выходных величин.

Нелинейные динамические системы такого рода удобно решать с помощью систем математического моделирования, в частности с помощью Matlab Simulink 6.5.0.1. Составленная с помощью этой программы модель позволяет выполнить математический расчет движения судна в реальном и ускоренном времени при различных управляющих и внешних воздействиях. Траектория движения центра тяжести судна отображается в виде графической зависимости. Кроме того, в ходе работы программы можно получить численное отображение выходных значений параметров, а также получить графики этих параметров на любом промежутке вычисления. При решении ДУ можно использовать ряд численных методов интегрирования (метод трапеций, метод Дорманда-Прайса, метод Розенброка). В основе большинства из этих методов лежит метод Рунге-Кутта. Модель имеет достаточно удобную структуру для внесения новых компонентов. Для того чтобы, например, заменить руль и винт рулевой насадкой, необходимо лишь удалить соответствующие блоки, содержащие уравнения сил и вставить новые. При этом можно создать базу данных, содержащую блоки и файлы расчета коэффициентов (для различных типов судов и вариантов моделирования).