Изучение и исследование колебаний распределенных конструкций

Подставляя поочередно значения k2, ., kn в уравнение (2.2.5.12), можно построить решения, соответствующее второму, третьему и т. д. собственным колебаниям:

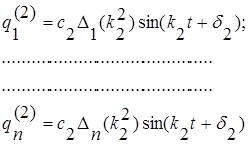(2.2.5.13)

и т. д. до

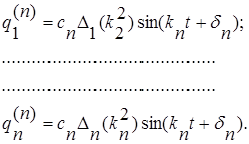(2.2.5.14)

Совокупности значений миноров 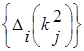образуют собственные формы j-х колебаний. Таким образом, каждой собственной частоте kj соответствует вполне определенная собственная форма колебания.

Общее решение системы (2.2.5.13) получим, складывая частные решения:

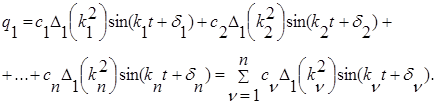(2.2.5.15)

Для произвольной координаты q j будем иметь

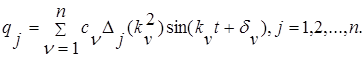(2.2.5.16)

Это решение содержит 2п произвольные постоянные c1, c2, …, cn и δ1,δ2, …,δn, которые определяются но заданным начальным условиям

из уравнений (2.2.5.16) при t=0 получаем

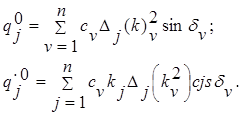(2.2.5.17)

Заметим, что исследование собственных или свободных колебаний в технических задачах сводится обычно к определению собственных частот k1, k2, …, kn из уравнения (2.2.5.3) и собственных форм

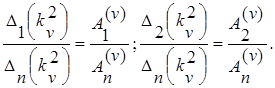
Если принять An = 1, то можно вычислить, во сколько раз амплитуды больше или меньше. При этом

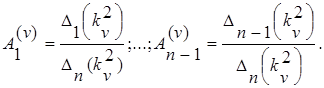(2.2.5.18)

Вынужденными называют колебания, обусловленные действием на механическую систему внешних периодических или импульсных сил.

В машинах возмущающими силами являются обычно силы инерции поступательно и вращательно движущихся масс. При нестационарных режимах работы машин (разгон, выбег) частоты и амплитуды возмущающих сил изменяются во времени. Вынужденные колебания, обусловленные действием возмущающих сил с переменной амплитудой и частотой, называются нестационарными.

Рассмотрим простейший случай вынужденных колебаний, когда действующие на систему силы Qj(t) являются гармоническими, имеют одинаковую частоту р и отличаются только амплитудами Hj, а диссипация энергии в системе отсутствует.

Уравнения вынужденных колебаний системы имеют в этом случае вид

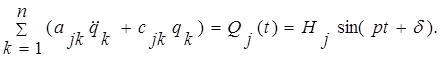(2.2.6.1)

Найдем частное решение, описывающее вынужденные колебания. Вынужденные колебания совершаются с частотой возмущающей силы, поэтому частные решения системы (2.2.6.1) находим в виде

(2.2.6.2)

Дифференцируя (2.2.6.2), получим

(2.2.6.3)

Подставляя выражения 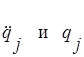в уравнения (2.2.6.1) и приравнивая коэффициенты при sin(pt+δ) в правых и левых частях уравнений, получим алгебраическую систему

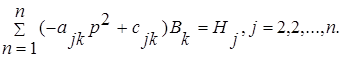(2.2.6.4)

Система (2.2.6.4) имеет нулевые решения B1, B2,…, Bn в случае, если определитель

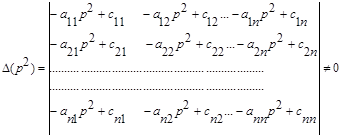(2.2.6.5)

Амплитуды в этом случае находятся по формуле Крамера:

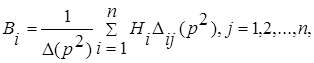(2.2.6.6)

где минор j-го столбца i-ой строки определителя.

Если что имеет место при совпадении частоты возмущающей силы с одной из собственных частот системы k1,k2,…,kn, уравнения (2.2.6.5) неразрешимы относительно Bj и решения уравнений (2.2.6.1) нельзя находить в виде (2.2.6.2).