Изучение и исследование колебаний распределенных конструкций

При p = kj,, j=1, 2, . n имеет место резонанс. При резонансе решение будет явно содержать время вне знака тригонометрической функции, вследствие чего отклонения системы от положения равновесия с течением времени будут неограниченно возрастать.

Для иллюстрации этого используем нормальные координаты, обозначив их. Приведенные к нормальным координатам уравнения вынужденных колебаний (2.2.6.1) можно представить в виде:

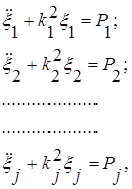(2.2.6.7)

где P1, Р2 ., Рn — обобщенные силы, отнесенные к нормальным координатам и обусловленные действием сил Q1, Q2, ., Qn

Обобщенные силы Р1(Р2, ., Р„ находят из условия равенства работ возмущающих сил в режиме соответствующего главного колебания.

Элементарная работа возмущающих сил Qj определяется по зависимости

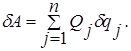(2.2.6.8)

Применяя формулы преобразования к главным координатам,

получим:

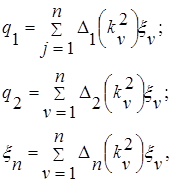(2.2.6.9)

где - миноры j-го столбца.

Вычисляя вариации δqj от выражений (2.2.6.9) и подставляя их в формулу (2.2.6.8), находим

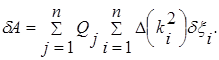(2.2.6.10)

В формуле (2.2.6.10) коэффициент при вариации δξi главной координаты ξi.

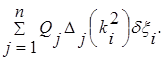(2.2.6.11)

представляет собой обобщенную силу, действующую на i-ю главную координату.

Предположим, что имеет место резонанс на s-й собственной частоте системы, т. е. р = ks, s = 1, 2, .,n. Соответствующее уравнение главного колебания с частотой ks имеет вид

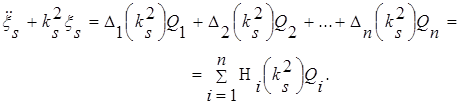(2.2.6.12)

Если возмущающие силы являются гармоническими, то уравнение (2.2.6.12) записывается в виде

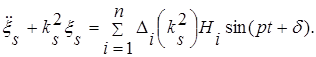(2.2.6.13)

Решение уравнения (2.2.6.13)

(2.2.6.14)

Представим sin(pt+δ) так:

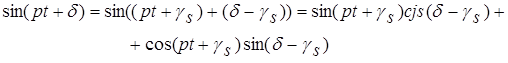
Найдём вторую производную по времени от выражения (2.2.6.14)

(2.2.6.16)

Подставляя выражения (2.2.6.14) и (2.2.6.16) в уравнение (2.2.6.12) и приравнивая в правой и левой частях коэффициенты при одинаковых тригонометрических функциях, получим (при ks = р) систему уравнений

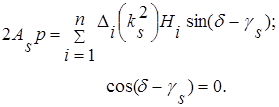(2.2.6.17)

Из уравнений (2.2.6.17) находим

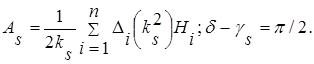
Подставляя AS в формулу (2.2.6.14) получим закон изменения S-ой главной координате при резонансе:

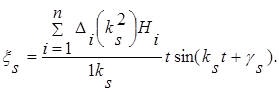(2.2.6.19)

Из формулы (2.2.6.18) следует, что амплитуда S-го главного колебания в случае резонанса (р = kS) при отсутствии сил сопротивления возрастает с течением времени.

Заметим, что нормальными координатами удобно пользоваться также и при исследовании вынужденных колебаний, возникающих в системе с n степенями свободы под действием возмущающих сил, являющихся произвольными функциями времени. В случае уравнения, приведённые к нормальным координатам, имеют вид:

(2.2.6.19)

где .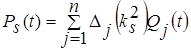

Для решения уравнений (2.2.6.19) можно воспользоваться методом вариаций произвольных постоянных.